Contents
General Logic
-
1. a deck of cards in a dark room
-
2. number of cars in a circular train
-
3. find the average salary
-
4. a hundred islanders with blue eyes
-
5. two eggs and a high-rise
-
6. a hundred passengers
-
7. special locations on Earth
-
8. the round lake redemption
-
9. the water level
-
10. lions and a sheep
Algorithms
-
1. identify the hiding employee
-
2. catch the rabbit
Probability & Statistics
-
1. gambling on coin flips
-
2. the expected number of traffic groups
-
3. a lonely mathematician
-
4. a sum of normals
-
5. three random variables with equal correlation
-
6. sampling with replacement
-
7. color changes
-
8. large-cycle permutations
-
9. prisoners
General Logic
1. A deck of cards in a dark room. You are given a deck of \(N\) cards with exactly \(k\) cards oriented face-down and others oriented face-up.
The value of \(k\) is known.
You are in a completely dark room and there is no way to tell the orientation of any card in the deck. Split the
deck into two not necessarily equal piles so that the number of cards face-down in each pile is the same.
Solution.
Solution.
Solution.
Solution.all such locations that you could start at.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
Solution.
-
Take
Solution.
-
Shut the light in the first car. The strategy is to progress in one direction relative to the first car, constantly turning the lights on and coming back to check if the first car still has its light off. More precisely, the algorithm is to (1) walk in one direction until you encounter a
car with a light off; assume this happens \(M\) cars down, (2) turn the light in that car on and return to the original car, (3) if the light is still off, continue to step (1). Otherwise, the last car you visited must be the first car; return \(M.\)
Solution.
-
Let the size of your team be \(N.\) Designate a person \(A_1\) to come up with some number, add their salary to it, and whisper the sum to person \(A_2.\) Next, the algorithm proceeds as follows: for all \(i\in\{2,3,\ldots,N\},\) person \(A_i\) adds their salary to the number they received from \(A_{i-1}\) and whispers the sum to person \(A_{i+1}.\) Person \(A_N\) would whisper their sum to person \(A_1,\) who finally subtracts his original number from the sum and announces the average salary.
Solution.
-
(50%). There are two solutions that, in my opinion, deserve discussion: one more formal but rather dull, and the other more clever but somewhat speculative.
For the first one, consider a more general problem with \(n\) passengers on a fully-booked plane with \(n\) seats. Denote the probability that the last passenger \(P_{n}\) occupies his assigned seat by \(p(n)\); the original problem asks for \(p(100).\)
To start, note that \(p(2) = 50\%.\) Now, let's find a recurrence relation for \(p(n).\) If the first passenger \(P_1\) takes his assigned seat, everything falls into order, and \(P_n\) gets his seat too. Otherwise, assume \(P_1\) takes a seat assigned to \(P_m\) where \(1 < m < n .\) Then, passengers \(P_2, P_3, \ldots, P_{m-1}\) will all get their seats, but \(P_m\) will have to choose one at random. His options are the seat of \(P_1\) union all seats that belong to passengers \(P_{m+1}, \ldots, P_{n}.\) This scenario corresponds to the same original problem with \(n-m+1\) total seats (where \(P_{m}\) choosing the seat of \(P_1\) corresponds to taking "the right" seat so that all others get their assigned seats thereafter, including \(P_n\)). Since \(P_1\) chooses a seat uniformly at random, we can write a recurrence relation
\[p(n) = \frac{1}{n}\left(2 + \sum_{m=2}^{n-2}{p(n-m+1)}\right)\]
where \(2 = 1 + 1\) comes from \(m=1\) (\(P_1\) takes his own seat) and \(m=n-1\) (\(P_n\) is guaranteed his seat). Assuming that \(p(k)=50\%,\) for all \(1 < k < n\) as an induction hypothesis, we compute \(p(n) = \frac{1}{n}(50\%\cdot(n-4) + 2) = 50\%.\)
A more elegant approach is to reformulate the boarding procedure in an equivalent but more intuitive way. As is likely to happen in real life, assume passengers \(P_2, P_3, \ldots, P_{n-1}\) each occupy their assigned seats and, in case it is already taken, kindly ask the squatter to move. While this will result in a different arrangement than in the original problem, it clearly does not affect the odds of the last passenger getting the correct seat. In this scenario, all passengers \(P_2\) through \(P_{n-1}\) sit in the right places while \(P_1\) is getting moved across the cabin unless he settles for his own seat or the seat of \(P_n.\) Each time someone kicks him out, \(P_1\) is equally likely to move to either of these two seats, so the probability that either of these two seats is available by the time \(P_n\) arrives should be the same by symmetry. Finally, note that these two seats are the only ones that can potentially remain unoccupied when \(P_n\) boards the flight.
Solution.
-
One obvious solution is the South pole; but there are more, infinitely many more. The other solutions are in the vicinity of the North pole so that moving 10 miles East comprises a full circle (or multiple circles) around the Earth. For this to happen, the original starting point should be 10 miles South of one of such concentric circles, so we first move up, make one or more loops (10 miles) around the North pole, and come back down.
Thus, the full solution is the South pole union a countable collection of
concentric circles around the North pole.
Solution.
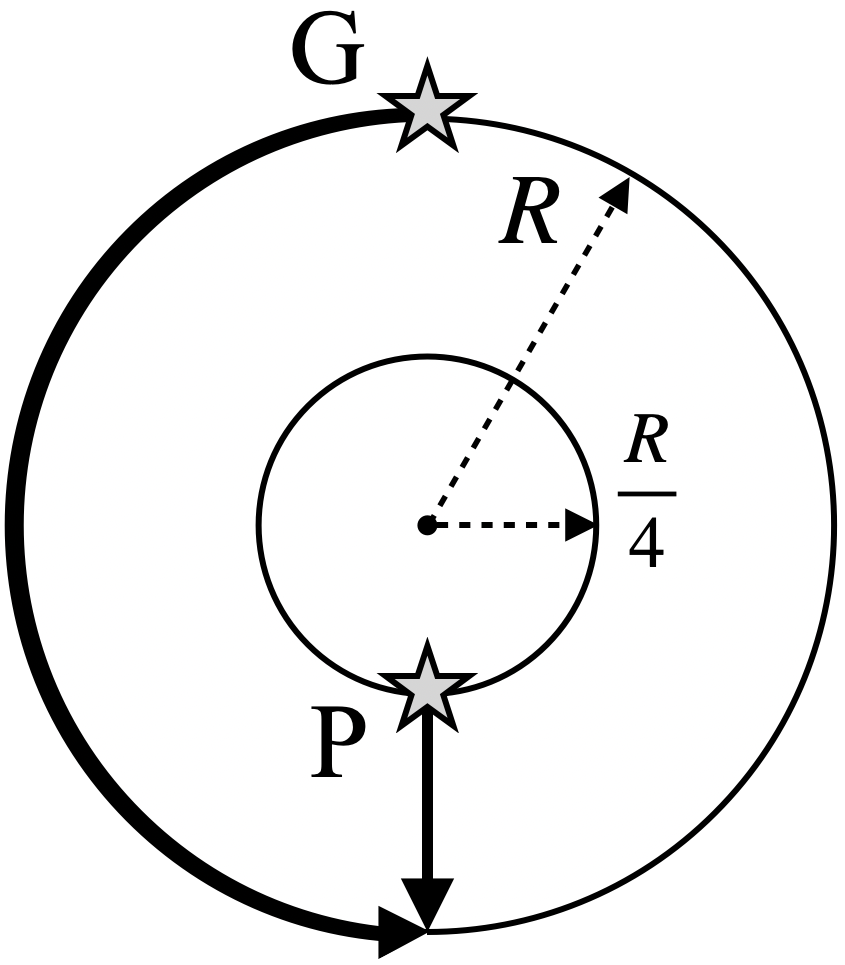 Since the ratio of their speeds is \(4,\) the angular velocity of the prisoner is larger than the angular velocity of the guard provided that the prisoner stays within the circle of radius \(R/4.\) It then follows that he can eventually get to be opposite to the guard on that circle (see the picture).
When this happens, the prisoner needs to swim \(\frac{3R}{4}\) to the nearest point on the ground whereas the guard must cover \(\pi R\) to get there. Therefore, the prisoner will be able to escape.
Since the ratio of their speeds is \(4,\) the angular velocity of the prisoner is larger than the angular velocity of the guard provided that the prisoner stays within the circle of radius \(R/4.\) It then follows that he can eventually get to be opposite to the guard on that circle (see the picture).
When this happens, the prisoner needs to swim \(\frac{3R}{4}\) to the nearest point on the ground whereas the guard must cover \(\pi R\) to get there. Therefore, the prisoner will be able to escape.
Solution.
-
If \(N=1,\) the lion eats the sheep. If \(N=2,\) the lion to eat the sheep first can be eaten by the other lion, which will certainly happen as there is no risk associated with it. Thus, no lion will eat the sheep if and only if \(N\) is even.
Algorithms
1. Identify the hiding employee. Each employee of a large corporation has a badge with a unique integer ID number. Every time an employee enters or leaves the office
building, they scan their badge at the gates, which gets registered in the daily logs. One day, exactly one employee stayed in the office overnight. Given the logs for that day, write an algorithm that finds the ID number of that employee in \(O(N)\) time and \(O(1)\)
extra space where \(N\) is the total number of employees.
Solution.
-
One naive linear-time and linear-space solution would be to use a hash table to store the number of times each ID appears in the logs and then traverse all its key-value pairs to find the one unmatched ID. However, due to the constant-space constraint, we can't use a hash table. In fact, this constraint makes it clear that data structures are useless here, and instead, we should come up with a clever
Solution.
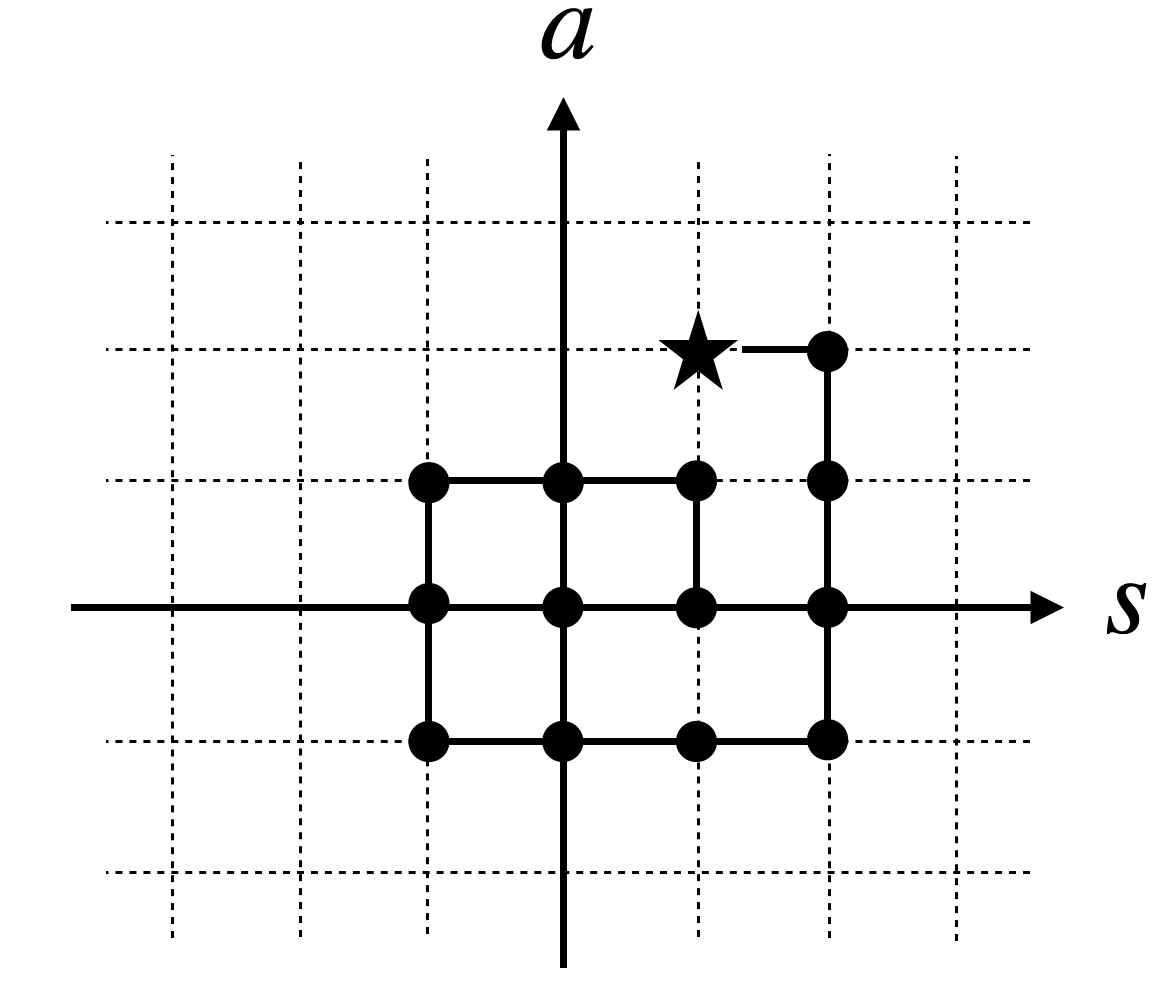 Let's factor the direction of the jumps into \(s\) by allowing it to be negative. Then, at any time \(t,\) the position of the rabbit is \(p(t)=a+st,\) so knowing both \(a\) and \(s\) is sufficient to catch the rabbit.
Therefore, we just need to come up with a strategy to identify \((a,s),\) which we can do iteratively starting with \((0,0)\) and progressing away from the origin in the \((a,s)\)-space. One such strategy is shown on the
picture (star represents the true values of \(s\) and \(a\)).
Let's factor the direction of the jumps into \(s\) by allowing it to be negative. Then, at any time \(t,\) the position of the rabbit is \(p(t)=a+st,\) so knowing both \(a\) and \(s\) is sufficient to catch the rabbit.
Therefore, we just need to come up with a strategy to identify \((a,s),\) which we can do iteratively starting with \((0,0)\) and progressing away from the origin in the \((a,s)\)-space. One such strategy is shown on the
picture (star represents the true values of \(s\) and \(a\)).
Probability & Statistics
1. Gambling on coin flips. You wander around the streets of St. Petersburg and notice a crowd of people watching a gambling game. The gambler pays the player $5 for every \(HT\) (heads, then tails) that comes up in a sequence of coin flips
that each costs $1. You observe the game long enough and find out that the game is, on average, profitable for the player. Inspired by his success, you dare to play yourself but the gambler suddenly wants to change the rules and pay you $5 for every \(HH\) (heads, then heads again) you throw. Note that
a sequence of three heads earns you only $5 unless followed by another heads. Would you agree to play the game on these terms?
2. The expected number of traffic groups. There are \(N\) cars at arbitrary locations on a one-dimensional road (no overtakes allowed). They all start moving at the same time in the same direction but
with different constant velocities that are independently drawn from a uniform distribution \(U[0,1].\) Once a faster car catches up with a slower car in front of it, it starts moving with that slower speed, and we say that these two cars
are now in the same traffic group (note that a single car following no other car and having no cars immediately behind it forms one traffic group). After some finite time,
this system reaches the limiting state where all potential traffic groups have been formed; denote this number of traffic groups by a random variable \(X.\) Find \(\mathbb{E}X.\)
3. A lonely mathematician. A lonely mathematician plays a drinking game with himself. In this game, every drink contains a random uniform \(U[0,1]\) amount of moonshine. Once the total consumed
amount of moonshine exceeds 1, the mathematician immediately falls asleep. Find the expected number of drinks needed to put the lonely mathematician to sleep.
Solution.
-
The best motivation to read through the solution is to know the final answer: it is the number \(e.\) We start by writing out the definition of expectation. Let \(X_i\sim\text{Unif}(0,1),\) then
\[\begin{align}\mathbb{E}(\text{number of drinks to sleep}) &= \sum_{n=2}^{\infty}n\mathbb{P}(\text{the critical drink is } X_{n}) = \sum_{n=2}^{\infty}n\mathbb{P}\left(\sum_{i=1}^{n-1}X_i<1, \sum_{i=1}^nX_i\geq 1\right)\\
&=\sum_{n=2}^{\infty}n\left[\mathbb{P}\left(\sum_{i=1}^{n-1}X_i<1\right)-\mathbb{P}\left(\sum_{i=1}^nX_i<1\right)\right]=\sum_{n=1}^{\infty}\mathbb{P}\left(\sum_{i=1}^nX_i<1\right).\end{align}\] Above we first used the fact
that events \(\{\sum_{i=1}^{n-1}X_i<1, \sum_{i=1}^{n}X_i\geq 1\}\) and \(\{\sum_{i=1}^nX_i<1\}\) are disjoint and their union is \(\{\sum_{i=1}^{n-1}X_i\},\) and then noticed that the resulting series is telescopic. Now, we find the
required probabilities via iterated integration: \[\mathbb{P}\left(\sum_{i=1}^nX_i<1\right)=\int_{0}^{1}\int_{0}^{1-x_1}\ldots\int_{0}^{1-\sum_{i=1}^{n-2}x_i}\int_{0}^{1-\sum_{i=1}^{n-1}x_i}dx_n\ldots dx_1=\int_{\Delta_n}dx_1\ldots dx_n\]
where we noted that this expression computes the volume of a \(n\)-dimensional simplex \(\Delta_n.\) A few low dimensional examples can give the right intuition. For \(n=2,\) \(\mathbb{P}(X_1+X_2<1)\) is the volume (area) of \(\Delta_2\)—a triangle with vertices \(\{(0,0), (0,1), (1,0)\},\) so \(\mathbb{P}(X_1+X_2<1) = 1/2.\) Likewise, \(\mathbb{P}(X_1+X_2+X_3<1) = \text{Vol}(\Delta_3) = 1/6\) as the volume of a tetrahedron.
In fact, induction shows that \(\text{Vol}(\Delta_n) = \frac{1}{n!}.\) Plugging this back into our series gives \(\sum_{n=1}^{\infty}\frac{1}{n!}=e.\)
Solution.
 I don't particularly like the wording of this question (it sounds intentionally informal) but this is how it was asked during an interview. Once you know the answer it is easy to reformulate the problem more rigorously, which takes some of its charm away.
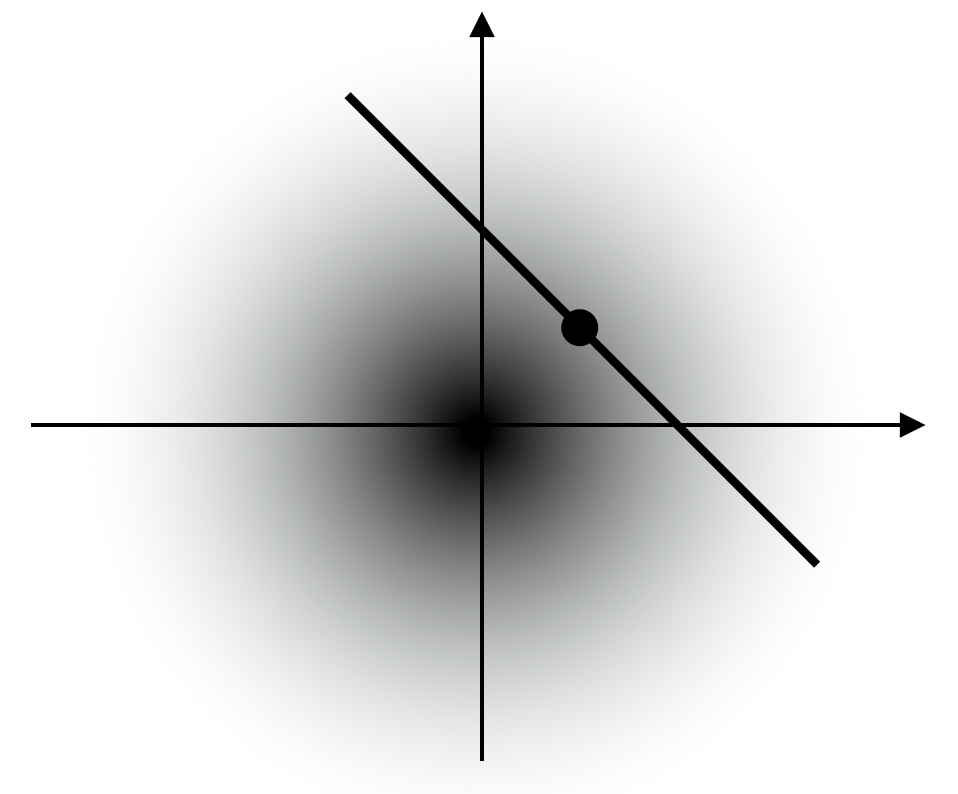
The informal language of the question hints towards a geometric argument. By visualizing the joint probability density function of two independent standard Gaussians and adding a linear constraint of \(x_2 = 1-x_1,\) we can see that \((0.5,0.5)\) is a reasonable estimate
for \((x_1,x_2\)) because it has the largest value of the PDF among all points on the line. That is, we just found the mode of a conditional distribution \((X_1,X_2)|S=1.\)
I don't particularly like the wording of this question (it sounds intentionally informal) but this is how it was asked during an interview. Once you know the answer it is easy to reformulate the problem more rigorously, which takes some of its charm away.
The informal language of the question hints towards a geometric argument. By visualizing the joint probability density function of two independent standard Gaussians and adding a linear constraint of \(x_2 = 1-x_1,\) we can see that \((0.5,0.5)\) is a reasonable estimate
for \((x_1,x_2\)) because it has the largest value of the PDF among all points on the line. That is, we just found the mode of a conditional distribution \((X_1,X_2)|S=1.\)
Solution.
-
Let \(Y_i\) (for \(i\in[N]\)) be an indicator variable indicating that the \(i\)-th object does not appear in the sample, and \(Y\) be the number of objects that do not appear in the sample, so \(X=N-Y\) and \(Y=\sum_{i=1}^NY_i.\) By linearity of expectation, \[\mathbb{E}X=N-\sum_{i=1}^N\mathbb{E}Y_i=N-\sum_{i=1}^N\mathbb{P}(Y_i=1)=N-N(1-\frac{1}{N})^k\] since \(\mathbb{E}Y_i=(1-\frac{1}{N})^k.\) Hence, \(\mathbb{E}X=N-N(1-\frac{1}{N})^k.\) Note that when \(k=N\rightarrow\infty,\) the proportion of unique objects in the sample is \(\lim_{N\rightarrow\infty}\left[1-(1-\frac{1}{N})^N\right]=1-\frac{1}{e}\approx 63\%.\)
Solution.
-
In this problem, we need to find the expected number (count) of some events. These types of problems can often be solved by defining indicator random variables for these simpler events and then using linearity of expectation to find the final answer. For this problem, we let \(X_i\) be the indicator variable with \(X_i = 1\) if the \(i\)-th drawn ball yields a color change (i.e., the \((i-1)\)-st ball is of the opposite color).
Then, we are interested in \(\mathbb{E}\left[\sum_{i=1}^{m+n}X_i\right] = \sum_{i=1}^{m+n}\mathbb{E}X_i\) while \(\mathbb{E}X_i = \mathbb{P}X_i.\) Thus, we just need to find the probability that the \(i\)-th drawn ball yields a color change. Intuitively, it should be equally likely to encounter a color change at any position \(i>1.\) To make it more rigorous, enumerate all balls in the jar and consider the space of all permutations \(S_{m+n}.\) For any pair of balls, there is the same number of permutations
with these balls at position \((1,2)\) and at position \((i-1,i).\) Thus, \(\mathbb{P}(X_i) = \mathbb{P}(X_2) = \frac{2mn}{(m+n)(m+n-1)}.\) Hence, the expected number of color changes is \(\frac{2mn}{m+n}.\)
Solution.
-
Clearly, there can only be one cycle of length larger that \(n/2\). Then, we can partition the collection of such permutations by the length \(k\) of their largest cycle, \(n/2 < k \leq n\).
There are \(\binom{n}{n-k}\) ways to select elements for that cycle, \((n-k-1)!\) ways to arrange them within the cycle, and \(k!\) ways to permute the remaining elements. This gives us \[\frac{n!}{(n-k)!k!}(n-k-1)!k!=\frac{n!}{n-k}\] permutations with a cycle of length \(k\).
Hence, there are \(n!\sum_{k=n/2}^{n} \frac{1}{n-k} = n!(H_n-H_{n/2})\) such permutations in total where \(H_n\) denotes the \(n\)-th Harmonic number. For the second part, we need to evaluate \(\lim_{n\rightarrow\infty}(H_n-H_{n/2})\).
Intuitively, this can be represented as the difference in the areas under hyperbola \(1/x\) when \(x=n\) and \(x=n/2\), respectively. To show this formally, we take a step back and rewrite \[H_n-H_{n/2} = \sum_{k=1}^{n}\frac{1}{k}-\sum_{k=1}^{n/2}\frac{1}{k}=\sum_{k=n/2}^{n}\frac{1}{k}=\sum_{k=n/2}^{n}\frac{2}{n}\frac{n}{2k}.\]
The factorization in the last step is needed to interpret the sum as a Darboux sum for the graph of \(f(x)=1/x\) over the interval \([1,2]\) partitioned into \(n/2\) chunks (width of each chunk is \(\frac{1}{n/2}\) and height of the \(i\)-th chunk is \(\frac{1}{1+\frac{i}{n/2}}\)). Clearly, this integral is \(\ln 2-\ln 1 = \ln 2.\)
Solution.
-
As a first baseline, let's compute the odds of survival when each prisoner checks half of the boxes randomly. Clearly, the probability that all \(100\) prisoners succeed is just \(\left(\frac{1}{2}\right)^{100}\). However, we can do better, considerably better. One slight improvement that most easily comes to mind is to partition boxes into two subsets of \(50\) and ask prisoners to choose either subset alternatingly. In this case, provided that all previous prisoners succeed, the subsequent prisoner will find his box with probability \(\frac{50}{99}\), bumping the overall
success probability to \(\frac{1}{2}\left(\frac{50}{99}\right)^{99}\). This might already be a significant improvement, but it's still vanishingly small. The key to a much better solution is to focus on the emergent structures of the random box arrangement itself. If a prisoner with identifier \(i\) starts with the \(i\)-th box and then sequentially checks the boxes in positions indicated by the number found inside of the previously opened one, the prisoner will effectively traverse the cycle containing his own box and, hence, will succeed if that cycle has length \(50\) or less.
If all prisoners use this strategy, they will all succed if and only if the box arrangement has no cycle longer than \(50,\) which happens with probability \(1-H_{100}+H_{50}\approx 1-\ln 2 \approx 0.31\) according to the

