Contents
Car fleets
In this etude, we cover variations (e.g., Leetcode #853 and #1776) of one famous problem.
At time \(t=0\), \(n\) cars start moving along a single-lane road (no overtakes allowed) from known locations and with known speeds, in one direction. Once a car catches up with a slower car in front, they form a fleet
and start moving together with the speed of the slower car. We will now consider a few interesting problems that arise in this setup. For simplicity, assume that
positions are presorted in increasing order, and
speeds are presorted accordingly. For each of the problems below, we would like to write a linear-time algorithm.
The number of fleets at \(t=\infty\) (easy). A natural question to ask is how many fleets will form once the configuration stabilizes. Note that the initial positions
of the cars don't matter since regardless of how far apart they may be, the faster cars will eventually catch up with the slower ones in front. In this brainteaser,
we computed the expected number of fleets with uniformly distributed car speeds. Note that a car is head of a fleet if and only if it is slower than all of the cars preceding it. Therefore, we just need to
count the number of such cars:
1 def numFleetsAtInfinity(speeds):
2 min_speed = float('inf')
3 num_fleets = 0
4 for speed in speeds[::-1]:
5 if speed < min_speed:
6 num_fleets += 1
7 min_speed = speed
8 return num_fleets
The number of fleets at destination (medium). This is Leetcode #853. In this problem,
we need to compute the number of fleets at mile
where the inequality in line 5 has to be strict to correctly handle the edge case specified in the problem statement.
destination (if a car becomes part of a fleet exactly at destination, it is considered one fleet).
Let's apply the same strategy—count the cars that are heads of their fleets. A car is head at destination if and only if its travel time to destination
is larger than that of any car in front of it. Therefore, the algorithm can be adapted as follows:
1 def numFleetsAtDestination(positions, speeds, destination):
2 max_time_to_dest = -float('inf')
3 num_fleets = 0
4 for position, speed in zip(positions[::-1], speeds[::-1]):
5 time_to_dest = (destination-position)/speed
6 if time_to_dest > max_time_to_dest:
7 num_fleets += 1
8 max_time_to_dest = time_to_dest
9 return num_fleets
The times of collisions (hard). This is Leetcode #1776. Let's refer to the event of a car joining a fleet as 'a collision'. In this part, we need to output an array indicating when each car will collide with the one in front,
or -1 if this will never happen. The complication here comes from the ambiguity in which car will cause a collision—this may depend on a variety of factors. For example, consider a scenario with three cars illustrated below.
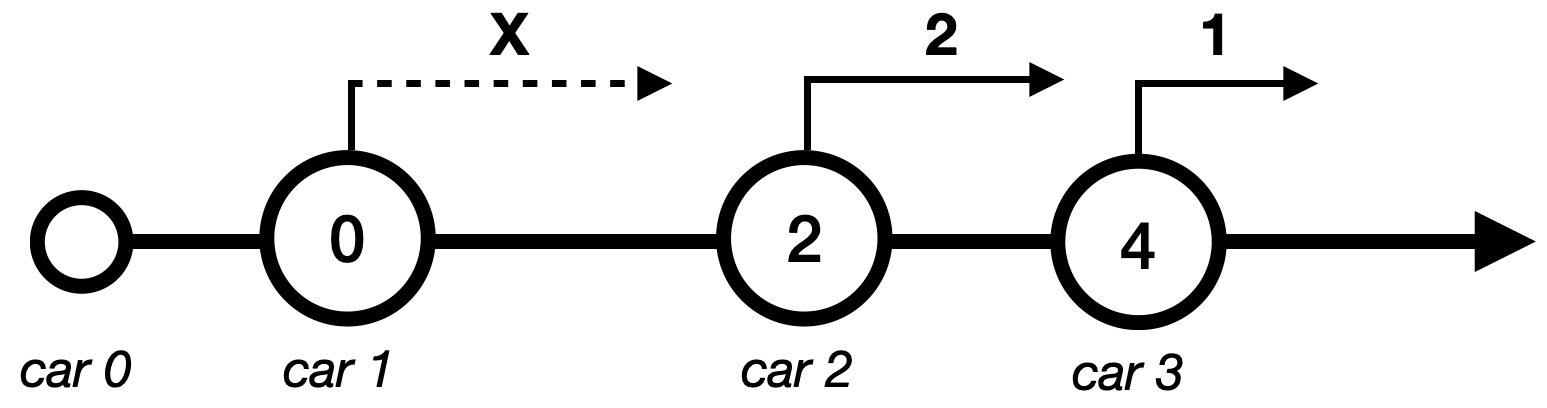In this example, car 2 collides with car 3 at \(t=2\). car 1 can collide with either car 2 if \(X>3\) or with car 3 (technically, with a fleet car 2 and car 3, but it's car 3's fault) if \(1< X < 3\).
Essentially, we need to compute the minimum "time-to-intersection" with any of the cars in front ignoring collisions (i.e., as if all cars continue with their initial speeds even after collision). Thus, it looks
like we need to iterate through all of these cars to compute the minimum, which would lead to an \(\mathcal{O}(n^2)\) algorithm; however, we can save some comparisons. In particular, we will show that if car 1 reaches car 3 before reaching car 2, then we don't need to consider car 2 for any of the subsequent cars (those behind car 1).
Let \(t_{12}\) be the time-to-intersection for car 1 and car 2 and \(t_{13}\) be the time-to-intersection for car 1 and car 3.
We let \(t_{13} < t_{12}\). First, note that (1) car 3 must clearly be slower than car 2 and (2) car 1 and car 3 are behind car 2 at the time of their intersection. Thus, in particular, for any \(t > t_{13}\), car 3 is behind car 2.
Now, assume that some car initially behind car 1 (say, car 0) would reach car 2 earlier than it would reach either car 1 or car 3. When could this happen? It must have happened after \(t_{12}\) for car 1 is originally between them. Hence, it must have
happened after car 1 intersected with car 3 because \(t_{13} < t_{12}\). However, at that time, car 3 is already behind car 2, so car 0 must have intersected with it first.
Therefore, our strategy is to keep a stack of cars still worth considering. We initialize it with the last car and, for every new car during backtracking, pop cars from the stack as long as the corresponding time-to-intersection decreases. If we encounter an increase in time-to-intersection, we stop our search as
there can't be a better car down the stack. At this time, we push the optimal car back into stack and add the one currently being processed as well.
The inequality in line 14 has to be non-strict to allow progression through the stack when the output of
1 def time(car, top):
2 if car[1]>top[1]:
3 d = top[0]-car[0]
4 v = car[1]-top[1]
5 return float(d)/v
6 else:
7 return float('inf')
8 def timesToCollision(positions, speeds):
9 cars = [[p,s] for p,s in zip(positions, speeds)]
10 stack = []
11 times = []
12 for car in cars[::-1]:
13 min_time = float('inf')
14 while len(stack)>0 and time(car, stack[-1]) <= min_time:
15 min_time = time(car, stack[-1])
16 min_car = stack.pop()
17 if min_time < float('inf'):
18 stack.append(min_car)
19 times.append(min_time)
20 else:
21 times.append(-1)
22 stack.append(car)
23 return times[::-1]
time(...) is infinity.
